All of us know the definitions of the sine and cosine ratios on the basis of sides of a right-angled triangle. Moreover, most of us probably know the unit circle definitions of the aforementioned ratios as well. However, in this post, I am going to be talking about another way of looking at the sine and cosine ratio: in terms of infinite series!
Ever wondered how calculators spit out values of the trig ratios for every angle you specify? Well, they make use of the infinite series expansion for the trigonometric ratios. When you use the first 5 to 6 terms of the infinite series, you can get a very close approximation to the actual value of the ratio at that angle. Another point that has to be noted is that these expansions only give out results when angles are measured in radians. A simple way of converting degrees to radians is by remembering the fact that 180 degrees = π radians.
Where does this series definition come from? Well, there exists a series expansion called the Taylor series, which is an expansion of a function based on a point a. The Taylor Series states that:
Ever wondered how calculators spit out values of the trig ratios for every angle you specify? Well, they make use of the infinite series expansion for the trigonometric ratios. When you use the first 5 to 6 terms of the infinite series, you can get a very close approximation to the actual value of the ratio at that angle. Another point that has to be noted is that these expansions only give out results when angles are measured in radians. A simple way of converting degrees to radians is by remembering the fact that 180 degrees = π radians.
Where does this series definition come from? Well, there exists a series expansion called the Taylor series, which is an expansion of a function based on a point a. The Taylor Series states that:
where, f to the power n means the nth derivative of a function f(x) at a.
In the special condition where a=0, the series is simplified and this simplified version is called the Maclaurin Series. When this is applied to f(x)= sin x, you get an infinite expansion that looks like this:
sin x = x – x 3/3! + x 5/5! – x7/7!... and so on.
In sigma notation, this becomes:
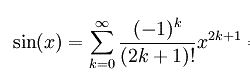 |
| Credits: blogs.ubc.ca |
Similarly, for cosine, the sigma notation is:
Isn’t it interesting?


